SPH 203,293 CEP CAT ONE Solved
(1) A resistance wire has a resistance value of 3.115 Ω at 27 0C. At what temperature will the resistance drop to 3 Ω? Take the temperature coefficient of the resistance wire as 4.2×10/0C.
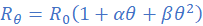 (i)
(i)
Since only the temperature coefficient is provided (can assume β=0), equation (i) may be reduced
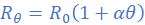 (ii)
(ii)
If Rθ = R1 at θ=θ1and Rθ = R2 at θ=θ2 it follows from equation (ii) that;
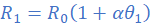 (iii)
(iii)
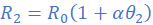 (iv)
(iv)
Dividing equation (i) by (ii) leads to;
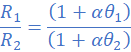
R1=3.115 Ω; θ1=27 0C; R2=3Ω; α=4.2×10/0C
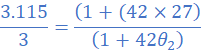
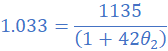
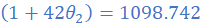
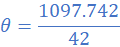
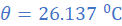
(2) A galvanometer across a thermocouple reads 0.9 V when the temperature difference between the cold and hot junction is 75 0C. If the cold junction temperature is increased by 15 0C, what will be the fractional change in EMF?
If E be the EMF and Δθ the temperature difference, then
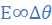
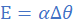
Where α is a constant of proportionality
Let E=E1 at Δθ=Δθ1 and E=E2 at Δθ=Δθ2. It follows that;
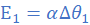 (i)
(i)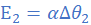 (ii)
(ii)
Dividing (i) with (ii)
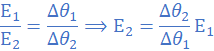
E1=0.9 V at Δθ1 = 75 0C and E=E2 at Δθ=75-15=60 0C
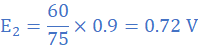
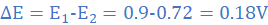
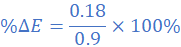
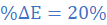
(3) A thermally insulated copper wire of length 19 cm and cross-sectional area 0.785 cm2 has one end at 100 0C and the other at 30 0C. Calculate the amount of heat that will flow in 600 s from the hot to the cold end of the wire. Take thermal conductivity of copper as 380 W/mK.
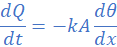
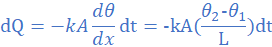
k=380 W/mK, A=0.785 cm2=785×10-7 m2, θ2=30 0C, θ1=100 0C, L=19 cm=0.19 m, dt=600s
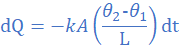
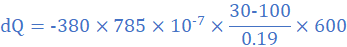
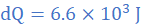
(4) A glass window pane of total area 0.5 m2 and thickness 0.6 cm has a temperature of 23 0C on the inside and 2 0C on the outside. Find the amount of heat conducted per hour. Take thermal conductivity of glass as 1.0 W/mk.
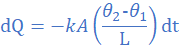
k=1.0 W/mK, A=0.5 m2, θ2=2 0C, θ1=23 0C, L=0.6 cm=0.006 m, dt=1 h=3600 s
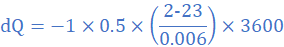
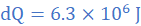
(5)When molten lead metal of mass 3 Kg and temperature 605 K is left to solidify, it is found that the temperature falls from 605 K to 600 K in 10s, remains constant at 600 K for a further 300 s before dropping to 595 K in 8.4 s. Assuming a constant heat loss and taking the specific heat capacity of solid lead as 140 J/kgK, find:
(a) the rate of loss of energy of lead
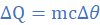
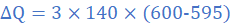
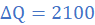
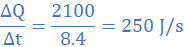
(b) the specific latent heat of fusion of lead
Heat lost in in 300 s equals product of rate of heat loss and time, ie


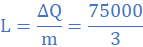
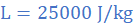
(c) the specific heat capacity of molten lead
Heat lost in in 10 s equals product of rate of heat loss and time, ie
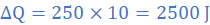
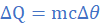
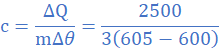
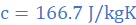


3 Comment(s)
Dennis Nzuvi katui (Sun, 30th Jul 2023, 4:01 PM)
Thankyou Dr. Hope my answer for question 3 which is 6594 won't be marked wrong as I can from the marking scheme the answer is 6.6 × 10^⁴ 6.594 × 10^⁴
Reply
Dennis Nzuvi katui (Sun, 30th Jul 2023, 4:01 PM)
Thankyou Dr. Hope my answer for question 3 which is 6594 won't be marked wrong as I can from the marking scheme the answer is 6.6 × 10^⁴ 6.594 × 10^⁴
Reply
Dr. Margaret W. Chege Author (Sun, 30th Jul 2023, 6:00 PM)
Answer on the marking scheme is 6.6x10^3 (rounded from 6594. You will not lose marks.
Reply