Equilibrium, Moment of force, Work and Machines

Equilibrium and centre of gravity

Center of gravity (cog) is the point on a body where the entire weight of the body acts. The lower the center of gravity, the more stable an object is. This means that it is more difficult to topple a stable object compared to an unstable one. One way of lowering the center of gravity of an object is by making the base relatively heavy.  Buses for example are constructed with luggage cabins on the lower sections, with limited load (carry-on luggage) being allowed in. 

Equilibrium

Consider a block of wood with the geometrical center as cog resting on its smaller surface. When a small amount of force is applied, the vertical line through the cog falls outside the base of the block and it topples over. 

When the block rests on the wider side, some small force will not topple the block since the vertical line through the cog still passes through its base.

There are three types of equilibrium

(i) Stable equilibrium

This occurs when a body displaced from the equilibrium position falls back to its initial position. Net torque (turning effect) of the body is opposite the direction of the applied force.  Example; a cone resting on its base:

Relatively short objects with heavy bases with large cross-sectional areas are associated with stable equilibrium.

(ii) Unstable equilibrium

This occurs when a body displaced from the position topples over when a small force is applied. Net torque (turning effect) of the body is in the same direction as the applied force.

Relatively tall objects with small bases and high centre of gravity are associated with unstable equilibrium.

(iii) Neutral equilibrium

This occurs when the equilibrium of a body is independent of the displacement from its initial position. The canter of gravity does not change even when an external force is applied.  Example a ball posses neutral equilibrium.

Examples

• A student climbing a hill tends to bend forward so as to shift the position of the centre of gravity to the front part to maintain equilibrium while one going down the hill tends to lean backward so as to shift the center of gravity to the backside in order to maintain balance.

A student carrying a heavy box using the right hand is observed to lean towards the left-hand side. This is because the box shifts the position of the centre of gravity of the system towards the right hand and consequently to balance moments and hence maintain balance, the student leans in the opposite direction. If the centre of gravity shifts, a force must be exerted in a direction opposite to that of the shift to maintain equilibrium.

Static equilibrium, moments of a force and turning effect of a force

A body is said to be in static equilibrium when it remains stationary despite being acted upon by forces. This happens when;

(1) The resultant force on the body is zero. 

This means that if all the forces acting on the body are resolved into vertical (up and down) and horizontal (left and right) components, the up-ward forces should be equal to the down-word forces, and the left-ward forces equal to the right-ward forces. 

(2) Clockwise moments must be equal to anticlockwise moments

Moment of a force is defined as the product of force and the perpendicular distance between the force and the point of support (pivot, fulcrum). 

Equilibrium (balance) occurs when:

From the diagram below, at equilibrium:

Turning effect of a force about a point occurs when clockwise moments do not balance anticlockwise movements. Example of turning effect of a force is closing a door. For turning effect to occur, the force should be applied at some distance from the pivot, and at an angle to the distance. 

The product of the force, say F, and the perpendicular distance from the pivot, say d, is equal to the torque τ, that is;

The greater the torque, the greater the turning effect. Hence, the turning effect increases with;

(i) increase in the force applied

(ii) increase in the distance between the force and the pivot. 

Work, power and Machines 

Work and power

In physics, work is said to be done when an applied force causes motion in the direction of force. Mathematically;

                  (i)

If the direction of force and the direction of motion are not the same, the force must be resolved into components and the appropriate component used. For example, suppose a force F is exerted on a body resting on a horizontal surface such that the body moves a horizontal distance d. Say the force is applied horizontally. 

It follows that the work done W will be;

                                                                                      (ii)

If now the force is applied at an angle θ to the horizontal and the body moves horizontally, the horizontal component of the force has to be obtained since it is this component that is doing work in the direction of motion.

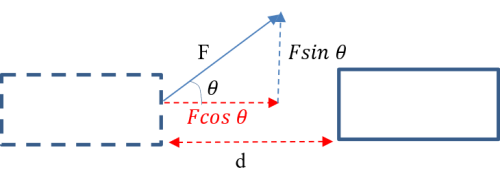
The work done in this case is given by;

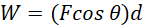                                                                           (iii)

The ability to do work is referred to as energy. There are many different types of energy among them mechanical energy (like the one described above), nuclear energy (in the form of alpha, beta and gamma radiation produced during radioactive decay) and electric energy by virtual of flowing charge. The work done per unit time or the amount of energy consumed per unit time is referred to as power, that is; 

                                                               (iv)

Work is often made easier by using a machine, for example using a crane, or a pulley, to lift a load. 

Machines are however not 100% efficient and as such the input work (work done by effort) is usually greater than the output work (work done by the load). This is because some of the input work is used to overcome friction and converted to heat, or is converted to sound. The ratio of the output work to the input work is called efficiency, often expressed in percentage form;

Machines: Pulleys and levers

Pulleys are mechanisms composed of a wheel (or multiple wheels) with a rope threaded over the wheels. One end of the rope supports the load while the other supports the effort. Pulleys are used to lift heavy objects for example at a construction site. 

The simplest pulley system is the ​Atwood's machine​, a single pulley system with two objects attached on either side of the pulley.  The objects can be of equal or unequal masses. Consider a frictionless Atwood’s pulley system consisting of two objects A and B of masses m₁ and m₂ respectively. Suppose B is moving downwards thereby pulling A upwards. Both masses have the same acceleration, say a, but in different directions. Say T be the tension in the rope.

Since mass A is accelerating upwards, the tension is greater than weight hence by Newton’s second law of motion:

                                              (i)

Mass B is accelerating downwards hence its weight is greater than tension. Thus;

                                              (ii)

Both tension T and acceleration a can be obtained using equations (i) and (ii) if other values are given.

A block and tackle pulley system consists of two or more pulleys with a rope or cable threaded between them. It is assembled in paired-pulley blocks with one pulley in one of the pairs fixed while the other one moves with the load.

Terms associated with pulleys 

(i) Effort: The force applied to overcome the load

(ii) Load: The force being overcome

Mechanical advantage (MA): This is defined as the ratio of the load (L) to the effort (E), that is:

                                                               (i)

(iii) Velocity ratio (VR): This is the ratio of distance travelled by the effort (d_E) to distance travelled by load (d_L);

                                                              (ii)

Velocity ratio is also equal to the number of ropes supporting the load (number of times the same rope runs through the moving block). Additionally, if the pulley system is used in such a way that the effort pulls downwards while the load moves upwards, velocity ratio is equal to the total number of pulleys in the system. 

Work input (W_in): This is the work done by the effort. It is the product of effort and effort distance, i.e.

                                                        (iii)

(iv) Work output (W_out): This is the work done on the load. It is the product of load and load distance, i.e., 

                                                      (iv)

(v) Efficiency: In reality, work input is always greater than work output because some of the work input is used to overcome friction and converted to heat, or is converted to sound. The ratio of work output to work input, often expressed as a percentage, is referred to as efficiency, i.e.

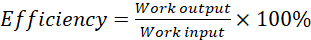        (v)    

By equations (iii) and (iv) equation (v) may be expressed as;

                       (vi)

                 (vii)

But 

and

hence;

                       (viii)

For an ideal pulley system where no energy is lost, the efficiency is 100%. In this case,

                                        (ix)

The maximum load that a pulley system that is 100% efficient can lift is therefore given as;

                                (x)

Example, pulleys given below are 100% efficient. Then;

A lever is basically a plank of wood pivoted somewhere in the middle with the effort arm (where the effort is applied) longer than the load arm (where the load is placed).

The mechanical advantage (MA) of the lever is 

Velocity ratio is defined as the ratio of the effort distance to the load distance or ratio of effort arm length to load arm length;

Efficiency is given by:

EXAMPLES

KCSE 2021

(1)  State the reason why a student climbing a hill tends to bend forward. (1 mark)

A student climbing a hill tends to bend forward so as to shift the position of the centre of gravity to the front part to maintain equilibrium.

(2)) State two conditions necessary for a body to be in equilibrium. (2 marks)

• Clockwise moments must be equal to anticlockwise moments
• The resultant force on the body should be zero.

(3) Figure 13 shows a non-uniform log of wood AB of length 4m. The log is held horizontally by applying forces of 80N at end A and 120N at end B.

Determine:

(a) the value of R. (1 mark)

(b) the position of the centre of gravity of the log from end B. (3 marks)

Since the log is balanced, the center of gravity coincides with the position of the pivot. If d be the distance between the pivot and B then the distance between pivot and A equals 4 - d.

(2) You are provided with the metre rule, a knife edge and a mass 𝑚₁. 

(a) Describe how the position of the centre of gravity of the metre rule can be determined using the knife edge. (2 marks)

An object balances when pivoted at its center of gravity. To determine the cog of the meter rule, the meter rule is placed on the knife edge. The location of the meter rule is then varied until it balances. The point of the knife edge corresponds with the cog of the rule.

(b) Using the position of centre of gravity determined in (a) and the mass 𝑚₁, describe how the mass M of the metre rule can be determined. (4 marks)

Note the position, say O, of the pivot on the meter rule. This is the point where the weight Mg of the meter rule acts.

Hang the mass m₁ to the left of O, say at point X. Move the pivot between points O and X until the meter rule balances (say at point Y). Determine the distance between X and Y (say a) and that between Y and O (say b).

Then use the equation

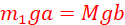
(3) Figure 7 shows a uniform rod AB 2m long and of mass 1 kg. It is pivoted 0.5m from end A and balanced horizontally by a string attached 0.1m from end B.

Determine the tension in the string. (𝑡𝑎𝑘𝑒 𝑔 = 10𝑁𝑘𝑔_⁻¹) (2 marks)

The weight W of the uniform bar acts downwards at its geometrical center O, that is 1 m from end A. distance of this point O from the pivot equals 1 - 0.5 = 0.5 m. The tension T acts upwards at a distance 2-  (0.1+0.5) = 1.4m from the pivot

(4) Figure 12 shows hydraulic lift system. The radius of the small piston is 5.64cm while that of the larger piston is 14.24cm. The small piston is operated using a lever. A force of 100N is applied to the lever.

Determine the:

 (a) pressure exerted by the smaller piston. (5 marks)

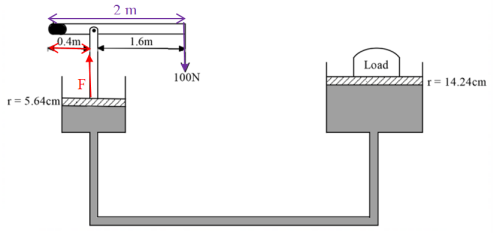
The force F on the lever arm produces anticlockwise moments about the hinge while the effort (= 100 N) produces clockwise moments about the same hinge.

Clockwise moments = anticlockwise moments

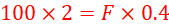
Area of the small piston

b) load that can be lifted. (3 marks)

Pressure generated at the smaller piston is distributed evenly to the larger piston. 

Area of the larger piston

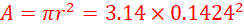
(c) mechanical advantage of the system. (3 marks

Example 2: KCSE 2020

(1) Figure 3 shows a traditional stool resting on a level surface.

(a) ldentify its state of equilibrium. ( 1 mark)

Stable equilibrium

(b) State the reason for the answer in (a). (1 mark)

A small amount of force tilts the object but when withdrawn, the object goes back to its initial equilibrium position.

(2)  Figure 4 shows a uniform rod AB of length 1m and weight 8N pivoted at 20 cm from one end. It is balanced by supporting it with a string attached to a fixed support.

The tension in the string is 4N. Determine the position of the string from end A. (3 marks)

Weight (W) acts downwards at the center (50 cm mark of the meter rule), a distance 30 cm from pivot and is responsible for clockwise moments. Tension (T), say at a distance d from the pivot acts upwards and is responsible for the anticlockwise moments.

60 cm from pivot (80 cm mark on the meter-rule)

(3) Figure 12 shows a simple machine.

On the same figure, mark and label the following parts:

(i) Effort and load arms (2 mark)

Solution

(4) Figure 13 shows a pulley system used to raise a mass of 5 kg through a height of 2 m when a force of 60N is applied. (Acceleration due to gravity g is 10ms^-2)

Determine the:

(a) distance moved by the effort   (1 mark)

VR=number of ropes supporting the load =2

5 kg through a height of 2 m when a force of 60N is applied

(b) work done on the load;(3 marks)

(c) potential energy gained by the load (g = 10 Nkg^-1). (1 mark)

KCSE 2019

(1) A student carrying a heavy box using the right fund is observed to lean towards the left-hand side. Explain this observation. (2 marks)

The box shifts the position of the center of gravity of the system towards the right hand and consequently to balance moments and hence maintain balance, the student leans in the opposite direction

(2) Figure 4 shows a one-meter-long uniform rod of negligible weight supporting two weights.

Determine the position of the fulcrum from O cm for the rod to remain in equilibrium. (3 marks)

The distance between the two loads equals 75 cm. Say d be the distance between 10 N load and the fulcrum, then the distance between the fulcrum equals 75 – d hence;

Equilibrium (balance) occurs when:

Fulcrum is 45 cm from the 10 N force of at the 50 cm mark of the meter rule.

(2) Figure 6 shows a bottle top opener being used to open a bottle.

Indicate on the diagram the direction of the load and the effort. (2 marks)

Solution

(3) A block and tackle system has three pulleys in the upper fixed block and two pulleys in the lower movable block.

(a) Draw a diagram to show how the system can be set up in order to lift a load and indicate the position of the load and effort. (3 marks)

Solution

(b) State the velocity ratio of the set up. (1 mark)

(c) In such a block and tackle system an effort of 200N is required to lift a load of 600 N. Determine its efficiency. (3 marks)

KCSE 2018

(1) Figure 7 shows an L-shaped wooden structure

On the diagram construct appropriate lines to show the position of the centre of gravity for the structure. (2 marks)

For a regularly shaped isotropic medium, cog corresponds to the geometrical center. The body is made of two regular parts. To obtain the cog of object, first obtain the geometrical center of each shape independent of the other. Draw a straight-line AB joining the two cogs. Draw a straight line XY joining the furthest corner, the corner at the interface and the line joining the cogs. The point where line XY cuts line AB is the cog of the system.

(2) An electric crane uses 8.0 x 10⁴ J of energy to lift a load of 2.0 X 10⁴ N in 4 s.

(a) Determine the;

(i) power developed by the crane, (3 marks)

output work = 8.0 x 10⁴ J, time= 4 s.

(ii) height to which the load is lifted, (2 marks)

(iii) efficiency of the crane whose motor is rated 2.5 X 10⁴ W. (2 marks)

(c ) State two forms of energy transformation that lead to the crane’s inefficiency. (2 marks)

• Heat
• sound

KCSE 2017

(1) Figure 1 shows a uniform wooden bar at equilibrium with two cans Y and Z of equal mass but different diameters.

The cans are simultaneously filled with equal volumes of water. Explain the observation made. (2 marks)

The fact that the wooden bar is in equilibrium (before water is introduced) means that the two cans are exerting equal forces downwards hence no turning effect. Equal volumes of water have the same mass and when simultaneously introduced, the cans still exert equal forces downwards and no turning effect occurs. The wooden bar therefore remains in equilibrium.

(2) A uniform metre rule is pivoted at its centre. Two weights of 20N and 10 N are suspended at the 20cm and 100cm marks respectively. Determine the position at which a 10N weight should be suspended in order to balance the system. (3 marks)

From the diagram below, at equilibrium:

For the meter rule in the question, equilibrium will not occur when the 20 N and 10 N are at 20 cm and 100 cm marks respectively given that;

. 

We assume the balance occurs when the 10 N force is at a distance d₂ from the pivot.

Since:

Hence;

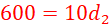
The 10 N force should be placed 60 cm from the pivot. This corresponds the 90 cm mark on the meter rule.

(2) Figure 3 shows two possible designs of a three-legged stool.

State a reason why B is more stable than A.

B is more stable because it has a lower center of gravity (cog). Center of gravity is the point on a body where the entire weight of the body acts. The lower the center of gravity, the more stable an object is. It is more difficult to topple a stable object compared to a non-stable object. 

Practice Questions

KCSE 2016

(1) . Figure 9 shows a uniform cardboard in the shape of a parallelogram.

Locate the centre of gravity of the cardboard. (1 mark)

(2) Define the term velocity ratio of a machine. (1 mark)

(3) Figure 12 shows part of a hydraulic press. The Plunger is the piston where effort is applied while the Ram piston is the position where the load is applied. The Plunger has cross-section area a m² while the Ram piston has cross-section, A m².

When the Plunger moves down a distance d the Ram piston moves up a distance D. Derive an expression for the Velocity Ratio (V.R.) in terms of A and a. (4 marks)

(3) A machine of velocity ratio 45 overcomes a load of 4.5 X 10³N when an effort of 135N is applied. Determine:

(a) the mechanical advantage (M.A) of the machine; (2 marks)

(b) efficiency of the machine; (2 marks)

(c) the percentage of the work that goes to waste. (1 mark)

KCSE 2015

(1) Figure 4 shows a uniform metal rod balanced at it’s centre by different forces.

Determine the value of T (3 marks)

(2) A person carrying a heavy luggage using one hand leans away from the luggage. State the reason for this. (1 mark)

(3) In a wheel and axle system, state the advantage of having a large wheel diameter compared to the axle diameter for a frictionless system. (1 mark)

KCSE 2014

(1) Figure 5 shows a uniform rod 4 m long and of mass 2 kg. It is pivoted 1 m from one end and balanced horizontally by a string attached near the other end.

Determine the position where a mass of 5 kg should be placed on the rod so that the rod remains horizontal and the tension in the string is Zero. (3 marks)

(2) Figure 6 shows two identical rods JK and LK connected with a hinge at K.

The position of the centre of gravity for the system is at P. The arrangement is now adjusted so that J and L move equal distances towards O. Sketch the new arrangement on the same diagram and mark the new position of the centre of gravity. (2 marks)

(3) Figure 10 shows a trolley of weight 20 N pulled by a force of 4 N from the bottom to the top of an inclined plane at a uniform speed.

(a)  State the value of the force acting downwards along the inclined plane.(1 mark)

(b) Explain how the value in pan (a) is obtained.(2 marks)

(c) For the system, determine the:

(i) mechanical advantage; (3 marks)

(ii) velocity ratio; (3 marks)

(iii) efficiency. (2 marks)

KCSE 2013

(1) State one factor that affects the turning effect of a force on a body. (1 mark)

(2) Figure 4 shows a uniform metre rule of weight I N with two weights of 0.18 N and 0.12 N suspended from its ends.

Figure 4

Determine how far from the 0.18 N weight a pivot should be placed in order to balance the meter rule. (3 marks)

(3) Figure 10 shows a pulley system used to raise a load by applying an effort of 500 N.

State the:

(a) velocity ratio of the system. (1 mark)

(b) purpose of pulley 2. (1 mark)

(c) Given that the machine has an efficiency of 80%, determine the maximum load that can be raised. (3 marks)

KCSE 2012

(1) A student pulls a block of wood along a horizontal surface by applying a constant force. State the reason why the block moves at a constant velocity. (1 mark)

(2) State the reason why a steel sphere resting on a horizontal surface said to be in neutral equilibrium. (1 mark)

(3) Figure 12 shows a set up used to determine the mass of a solid S. The rod is pivoted at its centre of gravity C.
         

(a) Name two measurements that need to be made to determine the mass of solid S. (1 mark)

(b) Write an expression to show how the measurement in (i) above are used to obtain the mass of S. (2 marks)

KCSE 2011

(1) Figure 1 shows a lorry moving on an inclined section of a straight road. At the back is a chain hanging from a point on a horizontal axis through the centreof gravity of the lorry.

State with a reason whether the lorry is stable or not stable. (1 mark)

(2) Figure 8 shows a uniform wooden block of mass 2kg and length 25cm lying on a bench. It hangs over the edge of the bench by 10cm. 

(a)  Indicate on the figure two forces acting on the wooden block. (1 mark)

(b) Determine the minimum force that can be applied on the wooden block to make it turn about the edge of the bench. (2 marks)

(3) Figure 16 shows a screw jack whose screw has a pitch of 1mm, and has a handle of 25 cm long.

Determine the velocity ratio of the jack. (3 marks)

KCSE 2010

(1) Figure 3 shows a uniform metre rule pivoted at the 30cm mark. it is balanced by a weight of2N suspended at the 5cm mark.

Figure 3

Determine the weight of the metre rule.         (2 marks)

Figure 6 shows an athlete lifting weights while standing with the feet apart.

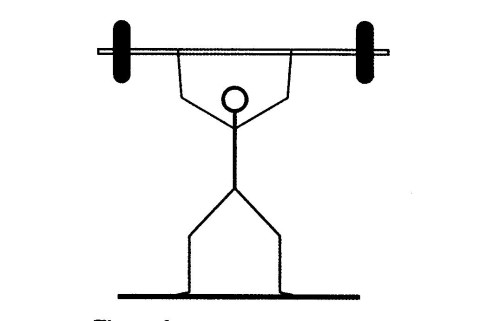
                                 Figure 6

Explain why standing with feet apart improves athletes' stability.

(2)  A cyclist initially at rest moved down a hill without pedalling. He applied brakes and eventually stopped. State the energy changes as the cyclist moved down the hill.         (1 mark)


 

Dr. Margaret W. Chege