Circular Motion

Circular motion refers to motion along a curved path e.g., a roundabout. Suppose an object moving along a circular path of radius r covers a distance s represented by the arclength AB (a section of the circumference of a circular path of a circle is referred to as arclength), sweeping an angle  about the center O.

The angle θ  swept by the particle (or the angle subtended at O by the arclength s) is called angular displacement. The SI unit of angular displacement is the radian, abbreviated as rad. 

Now, circumference c of the circular path is given by;

                                                         (i)

Equation (i) may be expressed as:

                                                            (ii)

If an object goes round the entire circumference, the curved distance (s) covered equals the circumference, i.e., s=c, while the angular displacement θ=2π. Bearing this in mind, equation (ii) may be generalised as;

                                                               (iii)

                                                            (iv)

It is important to note that;

                                           (v)

                                                (vi)

The rate of change of angular displacement with time is the angular velocity, ω, with units rad/s. Thus;

                                                              (vii)

Angular velocity is a vector quantity with direction given by the right-hand rule: imagine gripping the axis of rotation with the right hand with fingers curled in the direction of rotation; the thumb points in the direction of angular velocity. Angular velocity is always perpendicular to the plane of motion.  

The time taken by the object to complete 1 revolution is called period, T, with SI units seconds. Given that the angular displacement of an object after 1 revolution is equal to 2π , it follows that;

                                                            (viii)

                                                             (ix)

Frequency, f, with SI units Hertz, Hz, is the number of complete revolutions in unit time. It is also the reciprocal of period, i.e.

                                                               (x)

Using this in eq. (x) gives;   

                                                        (xi)

Linear velocity v (m/s) is the velocity the object would move at if for some reason it abruptly stopped moving in the circular path e.g., brakes failure of a car rounding a bend or moving in a roundabout, in which case the car would move in a straight line in accordance with Newton’s first law of motion. The linear velocity is usually tangential to the circular path.

If for example an object moves along the arclength AB of length s with linear velocity v, from definition of velocity, it follows that:

                                              (xi)

Since by equation (iv) s=rθ, equation (xi) may be expressed as;

                                               (xii)

From the definition of angular velocity, θ ⁄ t equal angular velocity ω. Equation (xii) may therefore be written as:

                                                              (xiii)

For a body to sustain circular motion, an external force must act on it. This force is called centripetal force, F_c, and is directed towards the center of the circular path.

For a body, mass m, moving with velocity v along a circular path radius r, the magnitude of the centripetal force Fc is given by:

                                                          (xiv)

Where;

                                                             (xv)

Where a is centripetal acceleration.

Object whirled in a circle

if the object is a stone tied to a string and swirled in a circle, the centripetal force is provided by the tension in the string. 

Suppose a stone, mass m, is tied to a string and swirled into a horizontal circle. Say the tension in the string is F. The weight of the stone, W=mg, acts vertically downward while the tension in the string is directed towards the center of the circular path.

At all points of the horizontal circular path, the weight and the tension are at right angles. This means that the weight of the object has no effect on the tension on the string.

Suppose the stone is now swirled in a vertical circle.

At points A and C, the weight of the stone has no impact on the tension. At point B, the weight of the stone acts vertically downwards while the centripetal force acts vertically upwards. The tension in the string is therefore maximum at B. At point D, both the weight and centripetal force act in the same direction. The tension in the string is therefore minimum at this point. 

NOTE: At points A and C (where the weight and tension are perpendicular to each other) the tension in the string is equal to the centripetal force, i.e.

                                                   (xvi)

Conditions necessary for a driver to negotiate a bend on a flat level road at a relatively high speed

A car of mass m moving at a speed v and negotiating a bend of radius r say round-about) experiences a centripetal force F directed towards the centre of the round-about.  The force is given by: 

The centripetal force keeps it within the circular path and without it, the vehicle would move in a straight line in accordance with Newton’s first law of motion (which states that a body at rest remains so while that in motion moves at a constant velocity in a straight line, unless acted upon by an external force). The centripetal force should be high for a driver to negotiate a bend properly. 

Since the centripetal force is provided to a large extent by the frictional force between the tyres and road, (i) the car tyres should have good treads (should not be smooth) to generate the required friction; (ii) Wider tyres are also better since they create more friction. 

Centripetal force constant, to counter the high speed (iii) the car should use the outer lane; (iv) the car should be made lighter. this also reduces the car's momentum making it easier to control.

(ii)The shorter the radius of the curve the greater the centripetal force. The driver should therefore use innermost lane to reduce radius of bend 

(iii) The heavier the car, the easier it is to negotiate a bend and as such extra weight can be added to the car to increase centripetal force.

Angle of banking (banking angle)

Centripetal force required by a car to navigate a bend on a level ground is provided by the frictional force between the car tyres and the road. The reliance on friction may however be reduced if the road is suitably banked by inclining it at an angle (called banking angle).

Consider a object, mass m, navigating a round-about of radius r at a linear speed v.  The object is under under the action of three forces: weight mg, normal reaction R and the centripetal force F_c = (mv²)/r. If the round-about is banked, say at an angle θ, the normal reaction R acquires a horizontal component equal to Rsin⁡θ.

Assuming no frictional force between the object and the ground, the horizontal component of the normal reaction provides the centripetal force required to keep the object in the circular path hence;

                        (i)

To determine the relationship between speed v, radius r and angle of banking  θ, we consider the vertical component of the normal reaction, Rcosθ. From the diagram above, it follows that

                       (ii)

Diving equation (i) by equation (ii);

            (iii)

Equation (iii) shows that (i) the bigger the banking angle the higher the velocity a vehicle can attain and still maintain the circular motion (radius constant). (ii) Banking angle constant, the vehicle should use the outermost lane to increase the radius. (iii) Velocity constant, a bigger banking angle is more appropriate   for a smaller roundabout.

NOTE:  A car negotiating a roundabout at progressively higher speed tends to move outwards.  The higher the speed, the higher the centripetal force required to keep the car in the  circular path. After a given speed within a given radius, the require centripetal force increases beyond the available frictional force between the car tyres and the the road. The car therefore moves outwards  to increase the radius of curvature thereby reducing the centripetal force required to sustain the circular motion. If the speed keeps increasing, the  car breaks away from the circular path and moves in a straight line in accordance with Newton's first law of motion, and also

Examples

KCSE 2021

(1) State two factors that affect the angular velocity of a body moving in a circular path. (2 marks) 

Factors affecting angular velocity;

• linear velocity v
• radium of the circular path

KCSE 2020

(1) Figure 8 shows a bucket filled with water and tied to one end of a string which is used to whirl it in a vertical circular path with a uniform speed v.

(a) State two forces acting on the bucket at any instant. (2 marks)

• Weight
• Tension

(b)) Explain why the tension is lowest at point A. (2 marks)

The weight and tension are in the same direction. Weight counters some of the tension hence the reduction in tension.

(c) The speed of the bucket is gradually reduced. Explain what is likely to be observed when the bucket is at point A. (2 marks)

When the bucket is rotating at high velocity, the centripetal force F_c (force towards the center is equal to centrifugal force F_f (force directed away from the center) in accordance with Newton’s third law of motion. It therefore follows that if m be the mass of the liquid and v the velocity, then;

For contents not to spill when the bucket is upside down (at point A),

Where mg is the weight of the bucket contents. As speed v reduces, the centrifugal force reduces. When;

the spillage occurs

(2) A stone of mass 40g is whirled at the end of a string in a horizontal circular path at (b) speed of 12ms^-1. (The string and the stone are in the same horizontal plane). If the string is 1m long, determine the tension in the string. (3 marks)

The radius of the circular path is equal to the length of the string hence;

KCSE 2019

(1) State the meaning of the term “radian” as a unit of measurement. ( 1 mark)

KCSE 2018

(1) Figure 4 shows a stone whirled in a vertical circle.

On the axes provided, sketch a graph of tension against time as the stone moves through point A, B, C and D. (3 marks)

Answer

KCSE 2017

(1) State three conditions necessary for a driver to negotiate a bend on a flat level road at a relatively high speed. (3 marks)

Solution

A car of mass m moving at a speed v and negotiating a bend of radius r (say round-about) experiences a centripetal force F directed towards the center of the round-about.  The force is given by: 

        (i)

The centripetal force keeps it within the circular path and without it, the vehicle would move in a straight line according to Newton’s first law of motion (which states that a body at rest remains so while that in motion moves at a constant velocity in a straight line, unless acted upon by an external force). The centripetal force should be high for a driver to negotiate a bend properly.  Thus;

(i) since the centripetal force is provided to a large extent by the frictional force between the tyres and road, the car tyres should have good treads (should not be smooth) to generate the required friction. Wider tyres are also better since they create more friction.

(ii)  The driver should therefore use outermost lane to increase radius of bend 

(iii) The car should be made lighter to reduce the momentum and increase control.

Practice Questions

KCSE 2016

(1) When a bus goes round a bend on a flat road, it experiences a centripetal force. State what provides the centripetal force. (1 mark)

(2) State the purpose of banking roads at bends. (2 marks)

KCSE 2015

(1) Figure 13 shows a pendulum bob suspended by a thread moving in a horizontal circle.

(i) Name two forces acting on the pendulum bob as it moves (2 marks)

(ii) State what happens to each of the forces when the angular velocity of the pendulum bob is increased. (2 marks)

(iii) State two applications of uniform circular motion in daily life. (2 marks)

KCSE 2014

(1) When a bus goes round a bend on a flat road, it experiences a centripetal force. State what provides the centripetal force. (1 mark)

(2) State the purpose of banking roads at bends. (1 mark)

(3) A student Whirls a stone of mass 0.2 kg tied to a string of length 0.4 m in a vertical plane at a constant speed of 2 revolutions per second.  

(a) State two forces acting on the stone when it is at the highest point. (2 marks)

(b) Determine the:

(i) angular velocity of the stone; (3 marks)

(ii) tension in the string when the stone is at the highest point; (3 marks)

(Take acceleration due to gravity g as 10 ms^-2)

KCSE 2013

(1) State two ways in which the centripetal force on a body of mass m can be increased (2 marks)

(2) Figure 7 shows an object at the end of a light spring balance connected to a peg using a string. The object is moving in a circular path on a smooth horizontal table with a constant speed

 (i) State what provides the centripetal force. (1 mark)

(ii) Indicate with an arrow on the figure the direction of the centripetal force. (1 mark)

(iii) State a reason why the object is accelerating while its speed remains constant. (1 mark)

(iv) Given that the mass of the object is 0.5 kg and it is moving at a speed of 8 ms^-1 at a radius of 2 m, determine the reading on the spring balance. (3 marks)

KCSE 2012

(1) Figure 10 shows the path of an object of mass m attached to a string of a length r when whirled in a vertical circle at a constant speed V. A is at the highest point on its path.

(a) State the forces that provide the centripetal force on the object when it is at point A. (2 marks)

(b) Indicate with an arrow on the diagram the direction of the net force F acting on the object when it is at A. (1 mark)

KCSE 2011

(1) Figure 10 shows a simple pendulum of length 80cm. The pendulum bob whose mass is 50g oscillates between points A and B, through its rest position C. A and B are both 10cm higher than C.

(a) (i) Indicate with an arrow, on the path ACB, the direction of the greatest velocity of the bob as it moves from A to BA (1 mark)

(ii) State the form of energy possessed by the pendulum bob at point A. (1 mark)

(b) Determine:

(i) the velocity of the bob at point C, (3 marks)

(ii) the tension in the string as the bob passes point C. (3 marks)

(take acceleration due to gravity g = 10 m/s²)

(c) After some time, the pendulum comes to rest at point C. State what happens to the energy it initially possessed.

(2) Figure 11 shows a stone attached to the end of a string with a uniform speed of 2m/s When the stone reaches point X on the circle, the string breaks.

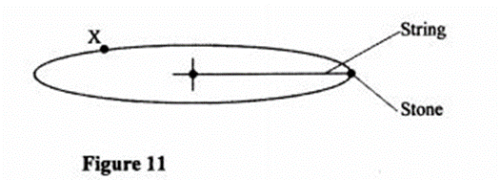
indicate on the diagram with an arrow, the direction of the motion of the stone when the string breaks. (1 mark)

(ii) State the magnitude of the velocity after the string breaks. (1 mark)

(iii) Give a reason for your answers in (i) and (ii). " (1 mark)

KCSE 2010

(1) Figure 5 shows a mass of 200g connected by a string through a hollow tube to a mass of 0.5kg. The 0.5kg mass is kept stationary in the air by whirling the 200g mass round in a horizontal circle of radius 1.0 metre.

Determine the angular velocity of the  200g mass.                (3 marks)

Dr. Margaret W. Chege