Pressure, Continuity and Bernoulli's principles
Pressure exerted by solids
Pressure refers to the force a body exerts perpendicularly per unit surface area i.e.
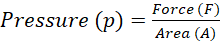 (i)
(i)
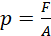 (ii)
(ii)
There are thus two factors that determine the pressure a solid exerts on a surface it is in contact with;
There are thus two factors that determine the pressure a solid exerts on a surface it is in contact with;
(i) Force (or weight); The more the force, the more the pressure and vice versa. If we consider two buddies, Biggi and Smolli, walking on the beach or on soft mud, and if Biggi with mass mb, is heavier than Smolli with mass ms, and assuming the area A of their feet in contact with the ground is equal, then, pressure pb exerted by Biggi will be;
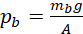
Pressure ps exerted by Smolli will be;
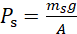
where g is the acceleration due to gravity. Since mb > ms it follows that Pb > Ps. Biggi will therefore sink deeper in the sand or in soft ground compared to Smolli.
(ii) Cross-sectional area; The smaller the cross-sectional area of contact, the greater the pressure and vice-versa. Someone in sharp pointed shoes sinks in soft mud or beach sand more than if he was wearing flat shoes. In nature, camels for example have broad hooves to prevent them from sinking in the soft sand, while elephants have flat ‘feet’ to prevent them from sinking in the ground owing to their massive weight.
Pressure exerted by liquids
Consider a closed rectangular tank of height h and cross-sectional area A (Figure 1). Suppose the tank is filled with a liquid, say water, of density ρ.

Figure 1
The pressure p the column of water exerts on the base of the tank is given by:
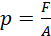
Now, the force F is equal to the weight W of the water column. If m be the mass of the water in the tank and g the acceleration due to gravity, then:
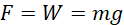 (iii)
(iii)
Hence;
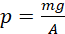 (iv)
(iv)
From definition of density and considering V to be the volume of water in the tank, it follows that;
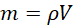 (v)
(v)
But;
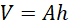 (vi)
(vi)
Hence;
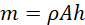 (vii)
(vii)
Using equation (vii) in equation (iv) leads to;
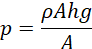
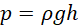 (viii)
(viii)
Equation(viii) is used to evaluate pressure exerted by liquids and gases (fluids). It shows that the pressure exerted is independent of the surface area. It however depends on:
(i) Density; The pressure exerted by a fluid is directly proportional to its density. For example, a column of water exerts more pressure on the base of a container compared to a column of paraffin of equal dimensions. A column of mercury on the other hand exerts more pressure than a column of water of equal dimensions. Mercury has a density of 13,546 kg/m3, water 1000 kg/m3 and oil (paraffin) 900 kg/m3.
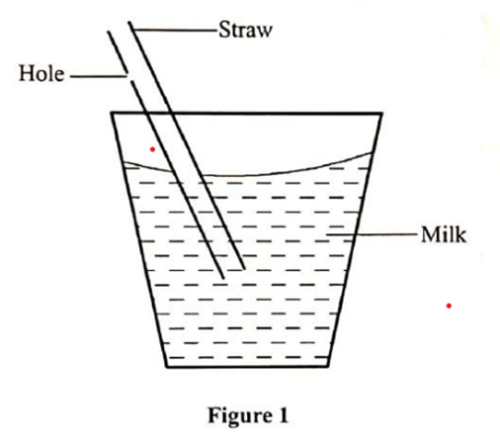
(ii) Height of the fluid column (depth); Pressure exerted by a fluid column increases with depth below the surface. For example, dams are constructed with thicker walls near the base to enable them withstand the relatively higher pressure. Additionally, if for example a long tube with vertical holes on the side is filled with water, the length of waterjet from the bottommost hole will be the longest due to the relatively high pressure, with the length of the waterjets gradually reducing as the holes get closer to the surface. This is illustrated in Figure 2.

Figure 2
Atmospheric pressure
As weird as it may sound, air has mass and therefore weight (force) as a result of gravitational attraction. The vertical force exerted on a surface by an air column as a result of gravitational attraction is referred to as atmospheric pressure or air pressure.
The pressure exerted by an air column of height h is given as;
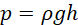
Where ρ is the density of the air column. The density of air on the earth’s surface is not uniform. At the sea level for instance, air molecules are more concentrated but as the elevation (altitude) increases, the concentration reduces. This means that density of air is higher at lower altitudes (for example Mombasa) compared to higher altitudes (for example Nairobi). Since pressure is directly proportional to density, it follows that atmospheric pressure reduces with altitude. Atmospheric pressure is maximum at the sea level with a value of 101,325 Pa.
Atmospheric pressure is commonly measured using a barometer. A barometer is simply a column of mercury in a glass tube inverted in an open vessel containing more mercury. The length of the mercury column is used to determine the magnitude of the atmospheric pressure. To make a simple mercury barometer, an evacuated tube (tube with air pumped out) is placed upside down in an open glass bowl containing mercury as shown in Figure 3.. The atmosphere exerts pressure on the surface of the mercury in the bowl but not in the tube given that it is sealed at the top. Considering that the tube is nearly at zero pressure, the higher atmospheric pressure pushes the mercury into the tube.
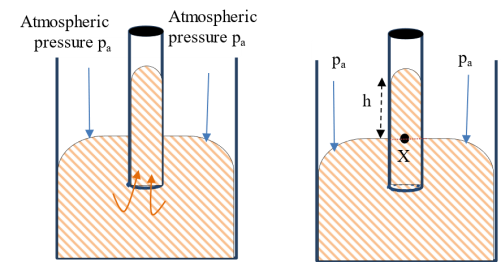
Figure 3
This ceases when the pressure the mercury column exerts at point X, which is at the same level as the mercury in the bowl, is equal to the atmospheric pressure. At sea level, the length of mercury the atmosphere can hold at normal temperature is 760 mm. Atmospheric pressure is therefore often given as 760 mmHg (760 mm of mercury). It is important to note that the atmosphere can hold longer columns of less dense liquids. For example, the atmosphere can hold a water column with a vertical height of up to 10.3 m.
An experiment normally used to demonstrate the existence of atmospheric pressure is the crashed can experiment. In the experiment, a metal can is partially filled with water and heated while open. Once the water starts boiling, the can is sealed, immediately removed from the heat, then left to cool down (or cold water poured on it to hasten the cooling process). It is observed that the metal can crashes as it cools down. This s illustrated in Figure 4.

Figure 4
The reason for this is that as the water heats up, the steam generated drives out the air in the metal can and takes its place and all through, the atmospheric pressure is equal to the pressure inside the open can. When the can is sealed and allowed to cool down, the vapour condenses (becomes water) thereby leaving a partial vacuum in the sealed can. At this point, the atmospheric pressure is greater than the pressure inside the can hence exerts force on the can crashing it in the process. It is important to note that atmospheric pressure (pa) acts equally in all directions.
To further illustrate the presence of atmospheric pressure, a glass tumbler is filled with a fluid, say water, and covered with a flat cardboard. While supporting the cardboard, the can is turned upside down after which the support is withdrawn (Figure 5)
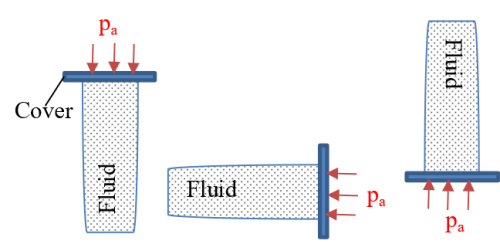
Figure 5
The water column, say of density ρ and height h, remains in the tumbler so long as the pressure it exerts on the cardboard cover is less than the atmospheric pressure i.e., ρgh < pa.
NOTE:
(i) The higher the pressure deference, the greater the impact. A can with less water would crash more as more air would have been pushed out by water vapour.
(ii) Pressure in a liquid is the same at all points at that level. For example, if tubes of different shapes, sizes, and orientation are dipped in a liquid, the rise of the liquid in all the tubes on account of atmospheric pressure will rest at the same horizontal level (Figure 6).
Figure 6
(iii) Suppose two open containers are connected via a tube with a tap as shown in Figure 7. Suppose too that with the tap closed, one of the containers has more water than the other.
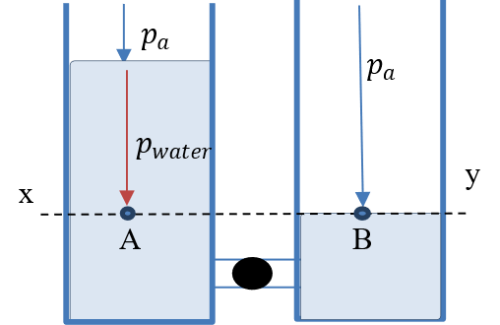
Figure 7
The pressure at A (pA) equals the atmospheric pressure (pa) plus the pressure due to the water column (pwater) while the pressure at B (pB) equals the pressure exerted by the atmosphere only, i.e.,
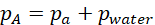 (i)
(i)
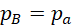 (ii)
(ii)
When the tap in the connecting pipe is opened, water flows from container A to container B on account of the pressure difference. The flow ceases when the pressure at points A and B are equal (Figure 8). This happens irrespective of the shape of the containers. This means that the pressure a liquid (or fluid) exerts at all points on the same horizontal level (xy) is equal.
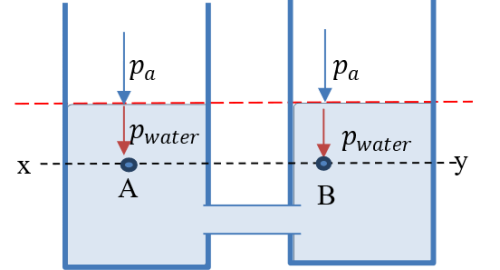
Figure 8
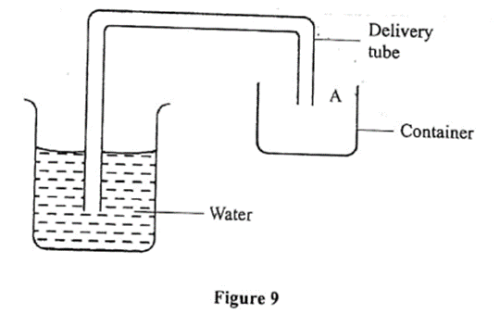
Syphon
A syphon is a tube that allows a liquid to move up the tube from a source, over the bend of the tube and down the longer limb (Figure 9).
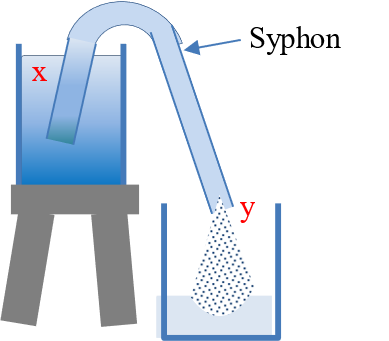
Figure 9
The water level (x) must however be at a higher level than the outlet (y) and the syphon be filled with water at the start of the siphoning. A combination of factors that include atmospheric pressure, gravity and cohesive force between the water molecules is said to be responsible for the movement of water (or any other liquid) through a syphon.
The water level (x) must however be at a higher level than the outlet (y) and the syphon be filled with water at the start of the siphoning. A combination of factors that include atmospheric pressure, gravity and cohesive force between the water molecules is said to be responsible for the movement of water (or any other liquid) through a syphon.
U-tube manometer
That pressure in a liquid is equal at all points at a given level is behind the working principle of a U-tube manometer, a device used for measuring pressure or comparing densities of two liquids. A U-tube manometer is simply a U-tube containing two immiscible liquids (liquids that do not mix) with the height of the liquid columns being used to determine the relative density of, or pressure exerted by, the liquid of interest.
Suppose a U-tube is partially filled with some liquid, say water (Figure 10). The water attains the same level in both tubes, X and Y.
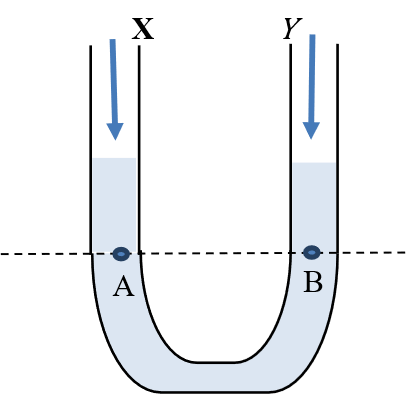
Figure 10
This means that points A and B are at the same pressure (equal to atmospheric pressure and pressure of the water column above the points). If air is blown into tube X, pressure at A exceeds that at B (Figure 11). Consequently, water will be pushed down tube X and up tube Y until the pressure at A balances that at B.
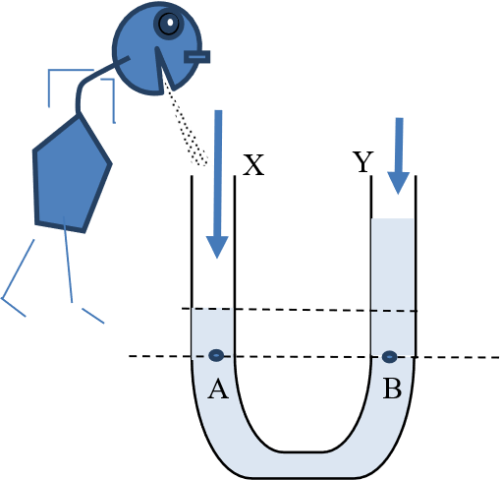
Figure 11
Suppose now instead of blowing into tube X, an immiscible liquid R of density ρR is gradually poured into the tube until it touches point A (Figure 12).
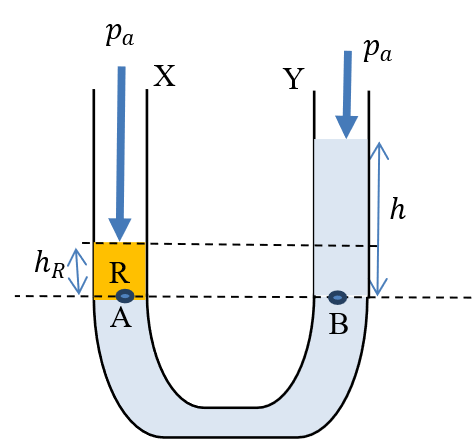
Figure 12
If the height of liquid R column be hR, the pressure at A (pA) is equal to the sum of the atmospheric pressure and the pressure exerted by the liquid R column, i.e.
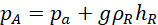 (i)
(i)
Considering that pressure at A is equal to the pressure at B, it follows that;
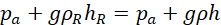 (iii)
(iii)
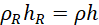 (iv)
(iv)
Since hR < h it follows that less of liquid R is required to give the same pressure as water. This means that the density of liquid R is greater than that of water.
Applications of atmospheric pressure
Syringe when used to draw a liquid: When the syringe piston is pushed down (before use) air in the syringe is pushed out. When the piston is pulled up (during use) pressure inside the syringe reduces and the higher atmospheric pressure pushes the liquid up into the syringe.
Straw: When a person sucks through a straw, the pressure in the straw reduces and the higher atmospheric pressure pushes the liquid up. A straw with a hole on the side cannot be used to draw up a liquid as air sucked out is balanced by air getting in through the hole. The pressure in the straw is therefore always equal to the atmospheric pressure.
Vacuum cleaner: When a vacuum cleaner is switched on, air is sucked out from inside the cleaner thereby reducing the pressure inside. The higher atmospheric pressure then forces air and dust particles into the cleaner.
Pascals principle
Pascal’s principle (Pascal’s law) states that for a liquid at rest and enclosed in a container, pressure applied at one point is equally transmitted throughout the liquid. Pascal law is applied for instant in a hydraulic press. The press is made up of a u-tube of different cross-sectional areas A1 (effort piston) and A2 (load piston) with A1 < A2. When a force F1 is applied in the smaller tube, the pressure p generated is given by;
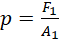 (i)
(i)
This pressure is distributed evenly throughout the liquid and consequently, a force F2 is generated at the load piston such that;
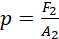 (ii)
(ii)
Equation (ii) implies that if A2 is large, F2 has to be equally large so as to keep the pressure constant.
Equations (i) and (ii) can be combined into a single equation as;
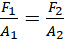 (iii)
(iii)
A small force at the effort piston generates a significantly large force at the load piston hence the load is easily compressed.
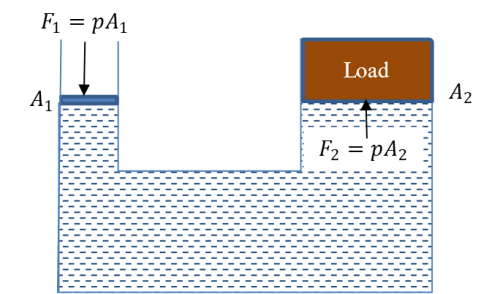
Figure 13
The same principle is also applied in hydraulic lift where a small amount of force (effort) generates a larger force that is used to lift a large load.
Continuity Equation and Bernoulli's Principle
Continuity equation is concerned with transport and conservation of mass. Imagine water flowing steadily in a pipe of different cross-section areas as shown. Let A1 and A2 be the cross-sectional areas of the wider (X) and narrower (Y) pipes, respectively. Suppose the two pipes are of equal length d as shown in Figure 1.
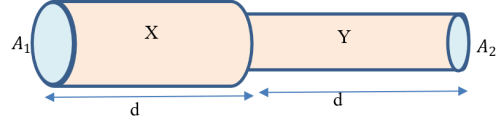
Figure 1
If in time t1 the wider pipe (X) is filled with water, then all that water must pass through the narrower pipe (Y) before X can fill-up with ‘new’ water again. This means that the volume flow rate, Vy (volume of water divided by time) of water in pipe Y must be equal to the volume flow rate Vx of water in pipe X, i.e.,
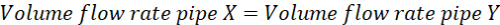 (i)
(i)
Now, if all the water that passed through pipe X in time t1 passes through pipe Y in time t2 , then;
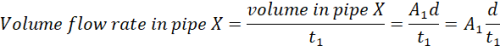 (ii)
(ii)
But;
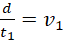
where v1 speed of water in X.
Hence;
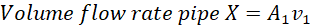 (iii)
(iii)
Similarly, volume flow rate in pipe Y is given by;
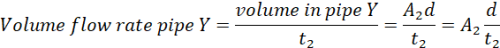 (iv)
(iv)
But
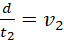
where v2 is the speed of water in Y. Hence;
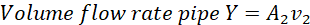 (v)
(v)
Equating equations (iii) and (v) leads to;
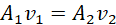 (vi)
(vi)
Equation (vi) represents the continuity equation. It implies that if A1 > A2 then v2 > v1. Put another way, when a liquid flows from a wider pipe to a narrower pipe, the speed of the liquid increases. This happens so as to maintain a constant volume flow rate of the liquid.
Equation (vi) is based on the assumptions that:
- Liquid is flowing steadily (no turbulence as this would lead to an increase in pressure)
- Liquid is not compressible
- Liquid is non-viscous so as to reduce frictional drag. Examples of non-viscous liquids include water, petrol, paraffin etc. An example of a viscous liquid is glycerine.
Bernoulli’s principle is concerned with transport and conservation of energy that include kinetic energy, gravitational potential energy and energy on account of pressure.
Consider a liquid flowing in a pipe of different cross-sectional areas and at different elevations from a reference point as shown in Figure 2.
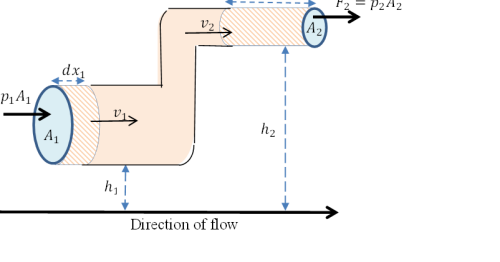
Figure 2
The liquid possesses energy in three forms;
Kinetic energy, K
Gravitational potential energy, U
Work due to pressure, W
Kinetic energy, K
Suppose in time t, a liquid of mass m and density ρ moves through a small distance dx1 in the wide pipe with velocity v1. When the liquid flows into the narrow pipe, the velocity increases, say to v2 in accordance with the continuity equation, covering a distance dx2 within time t (time t constant hence dx2 > dx1). The change in kinetic energy ∆K when the liquid moves from the wider to the narrow pipe becomes;
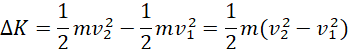 (vii)
(vii)
But
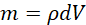
and
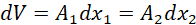
where dV the volume of the liquid that has moved through the pipe in time t. Hence;
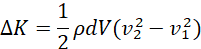 (viii)
(viii)
Gravitational potential energy, U.
The liquid in the wide and narrow pipes possess potential energy by virtual of their elevation. If h1 and h2 be the elevations of the liquids in the wide and narrow pipes respectively, then the change in potential energy ∆U when the liquid flows from the wide to the narrow pipe is given by:
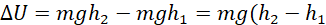 ) (ix)
) (ix)
Since
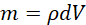
Then
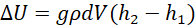 (x)
(x)
Work due to pressure, W
Suppose the liquid in the wide pipe is under pressure p1. This pressure generates force F1 considering;
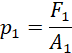 (xi)
(xi)
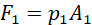 (xii)
(xii)
Similarly, if p2 be the pressure of the liquid in the narrow pipe and F2 the force generated, then;
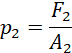 (xiii)
(xiii)
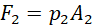 (xiv)
(xiv)
The forces F1 and F2 drive the liquid through distances dx1 and dx2 respectively and therefore do work equal to the product of the force and the respective distance. The change in the work done ∆Wp on account of pressure is therefore equal to;
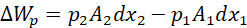 (xv)
(xv)
But
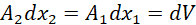
Hence;
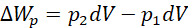 (xvii)
(xvii)
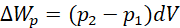 (xviii)
(xviii)
Now, considering that the total energy of the system is conserved, it follows that no change in total energy occurs as the liquid moves from the wide to the narrow pipe (energy is conserved). The total change in energy therefore equals zero, that is;
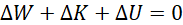 (xix)
(xix)
Using equations (viii), (x) and (xviii) in equation (xix) leads to;
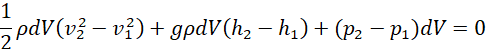
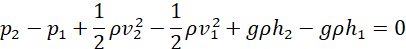
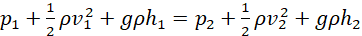 (xx)
(xx)
In general, equation (xxii) may be expressed as;
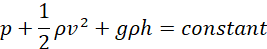 (xxi)
(xxi)
Equation (xxi) is a mathematical representation of Bernoulli’s Principle. It shows that a reduction in the speed of a fluid leads to an increase in pressure.
NOTE: Motion of a fluid is represented by lines called streamlines. If the streamlines are close together, speed is high and pressure is low. If far apart, speed is low hence pressure is high.
Implications of Bernoulli’s principle
(1) Consider a liquid flowing in a pipe of different cross-sectional areas A1, A2 and A3 where A1>A2>A3, with velocities v1, v2 and v3 respectively. Suppose too that tubes 1,2 and 3 are fixed in the sections of the pipe with cross section areas A1 A2 and A3respectively. If the atmospheric pressure is lower than the liquid pressure, the higher liquid pressure pushes the liquid up the tubes with the liquid attaining the highest level in tube 1, followed by tube 2 and lastly tube 3. This is illustrated in Figure 3.
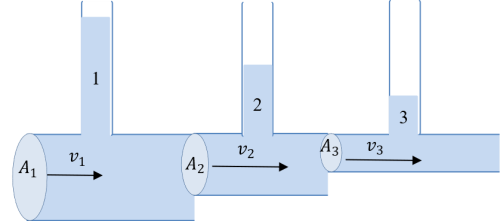
Figure 3
According to the continuity equation
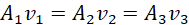
This means that\ since A1>A2>A3 then v1<v2<v3 . By Bernoulli’s equation (assuming h to be negligible);
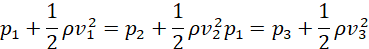
Since v1 < v2 < v3, then p 1> p2 >p3. Liquid pressure increases with the cross- sectional area and therefore that the liquid attains the highest level in tube 1.
(2) A speeding car appears to fly (barely touch the ground). This is because the speed of air above the car is higher than under the car leading to regions of low and high pressure respectively, with the higher pressure forcing the car upwards. This is illustrated in Figure 4.
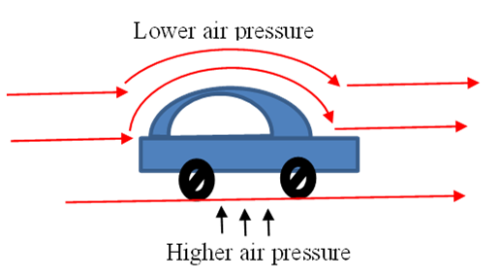
Figure 4
(4) Rooftops are blown away during wind storms due to lower pressure over the roof compared to inside the house.
(5) Vegetation bends towards busy roads because speeding cars create a region of low pressure near the road. The higher pressure on the other side of the vegetation pushes the vegetation towards the road.
(6) When air is blown between two papers, the papers move closer as pressure between them reduces.
EXAMPLES
Examples 1 KCSE 2021
(1) Figure 2 shows a siphon used to empty a tank.
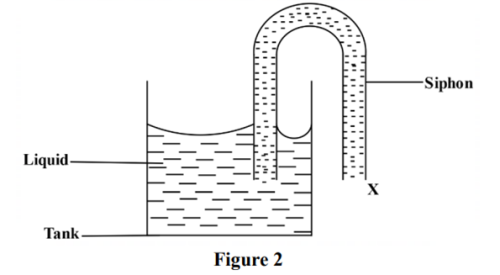
In order to start the siphon, state why:
(a) it must be full of liquid (1 mark)
Answer: The syphon should be filled with the liquid to drive out air hence remove the effect of atmospheric pressure which would otherwise prevent water from flowing out as pressure inside the tube would be equal to pressure outside the tube.
(b) End X must be below the level of the liquid in the tank (1 mark
Answer: To create pressure difference
(2) Figure 9 shows a folded piece of paper. A stream of air is blown underneath the paper.
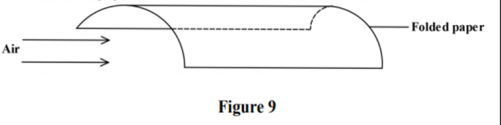
Explain why the paper collapsed. (2 marks)
Answer: When air is blown underneath the paper, the air molecules are forced to move faster thereby creating a region of lower pressure in accordance with Bernoulli’s principle. The higher atmospheric pressure above the paper forces it downwards hence the collapse.
(3) Figure 12 shows hydraulic lift system. The radius of the small piston is 5.64cm while that of the larger piston is 14.24cm. The small piston is operated using a lever. A force of 100N is applied to the lever.
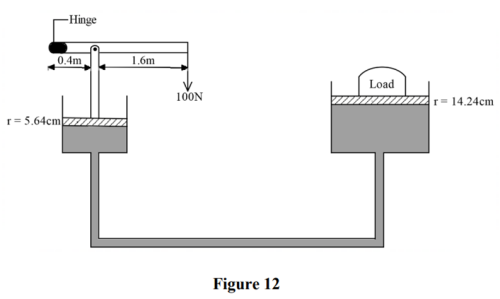
Determine the:
(a) pressure exerted by the smaller piston. (5 marks)
Solution
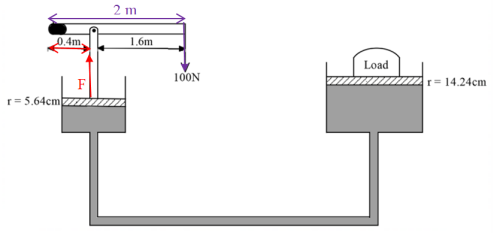
The force F on the lever arm produces anticlockwise moments about the hinge while the effort (= 100 N) produces clockwise moments about the same hinge.
Clockwise moments = anticlockwise moments
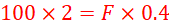
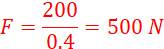
Area of the small piston A is give by;
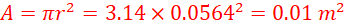
Hence
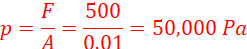
b) load that can be lifted. (3 marks)
Solution
Pressure generated at the smaller piston is distributed evenly to the larger piston.

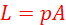
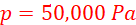
Area of larger piston
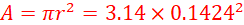
Hence
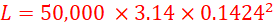
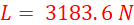
c) mechanical advantage of the system. (3 marks)
Solution
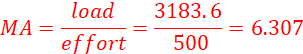
Example 2: KCSE 2020
(1) Figure 2 shows the scale of a measuring instrument.
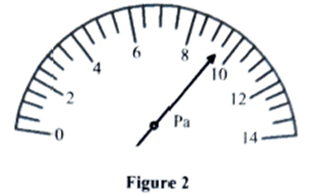
(a) State the physical quantity measured by this instrument. (1 mark)
Answer: Pressure because the units of measurement are Pascal (Pa)
(b) Determine the reading indicated. (1 mark)
Solution
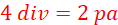
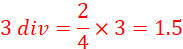
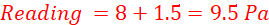
(2) Figure 5 shows a roof of a house over which wind is blowing.
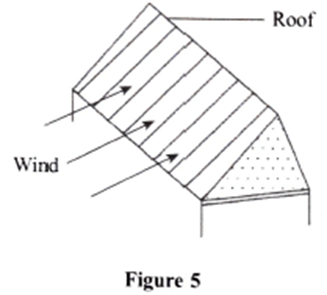
It was observed that, when the speed of the wind increased, the roof was blown off. Explain this observation. (2 marks)
Answer: The speed of air particles above the roof increases creating a region of low pressure in line with Bernoulli’s principle. The higher pressure indoors forces the roof off the building.
(3) Figure 9 shows a setup used by a student to investigate how a siphon works.
(a) State what would be observed when the student sucks the tube at point A and releases it. (2 marks)
Answer: Liquid moves up the tube but moves back down when the student stops blowing (the liquid does not flow out)
(b) Explain the observation in (a) above. (2 marks)
Answer: The outlet is above the inlet hence no pressure difference. The atmospheric pressure is not sufficient to move liquid over the bend.
(4) Figure 10 shows a test-tube inverted and floating inside a plastic bottle containing some water. The bottle is then sealed.
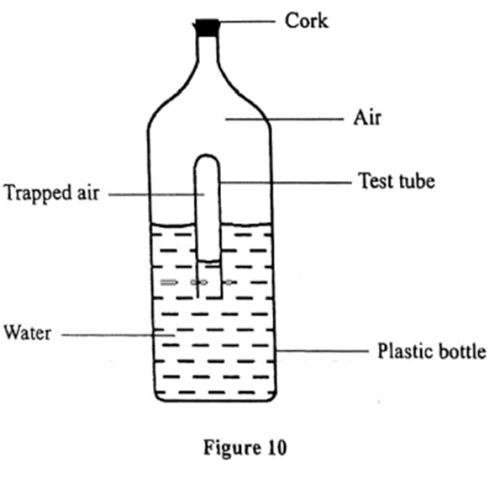
It is observed that when the sides of the bottle are squeezed, the test-rube sinks. Explain this observation. (3 marks)
Answer: When the sides are squeezed, air pressure inside the bottle increases. The high air pressure forces the liquid up the test tube. Test tube gains weight and therefore sinks.
(5) A metallic box weighs 188N and measures 10cm by 30 cm by 8 cm. Determine the maximum pressure it can exert when lying on one of its surfaces. (3 marks)
Solution
From the definition of pressure;
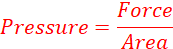
Pressure is maximum when the box is lying on its smallest side (side with least cross-sectional area).
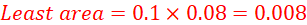

Example 3 KCSE 2019
(1) It was observed that upon sucking the straw, milk did not rise up the straw. Explain this observation. (2 marks)
Answer: A straw with a hole on the side cannot be used to draw up a liquid as air sucked out is balanced by air getting in through the hole. The pressure in the straw is therefore always equal to the atmospheric pressure.
(2) For a fluid flowing at a velocity V in a tube of cross-sectional area A, VA = constant; State the assumptions=made in deriving this equation. (2 marks)
Answer: Flowing steadily. Incompressible, Non-viscous
Example 4 KCSE 2018
(1) . Figure 2 shows an instrument used to measure atmospheric pressure
State with a reason the modification that would be required in a similar set-up if mercury were to be replaced with water. (2 marks)
Answer: Modification that would be required in a similar set-up if mercury were to be replaced with water – use a much longer tube. The density of water is lower hence the atmosphere can hold a much longer column.
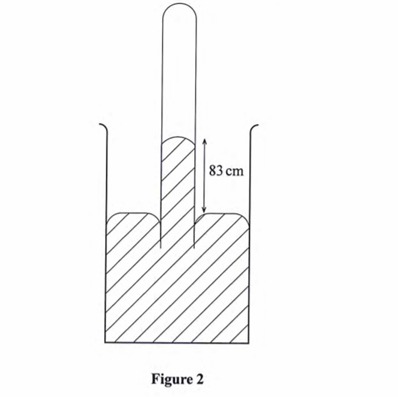
(2) Figure 10 shows heights of two immiscible liquids X and Y in a U-tube (drawn to scale).
(i) State with a reason which of the two liquids X and Y has a higher density.
(2 marks)
Answer
The liquid column above A is shorter than the liquid column above B.
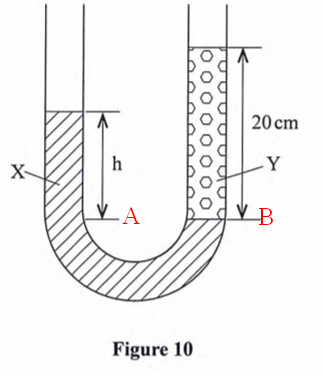
This means that liquid X is denser given that less of it is required to give the same pressure at point A (which is equal to pressure at B)
(ii) Determine the value of h. (2 marks)
Since drawn to scale: h=12 cm
iii) Given that the density of liquid Y is p, write down an expression for the density d of liquid x in terms of p. (2 marks)



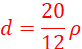
(3) a) With the aid of a diagram, describe how a liquid may be siphoned from one container to another using a flexible tube. (3 marks)
Dip one end (inlet) of the syphon in the liquid. Arrange the empty container in such a way that the other end (outlet) of the syphon is at a lower level relative to the inlet. Ensure that the syphon is filled with the liquid (can suck at the outlet until the liquid starts flowing out).

b)State one application of the siphon. (1 mark)
- Drinking straw,
- Transferring water from one container to the next
(4) Figure 5 shows a ball spinning as it moves.
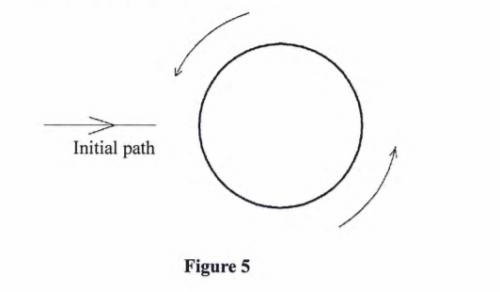
(a) On the diagram, sketch the path followed by the ball as it moves. (1 mark)
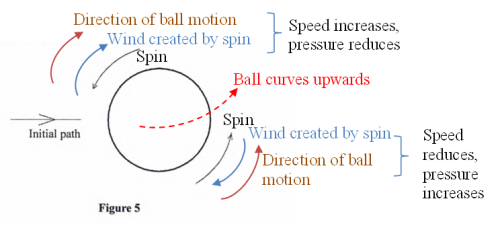
Curves upwards
(b) Explain why the ball takes that path. (3 marks)
Bernoulli’s principle
At the upper part, the spin of the ball is opposite the direction of motion of the ball. This causes the air above the ball to move in the opposite direction (and in the direction of the moving ball). The effective speed of the upper side of the ball and hence that of the air around it increases and pressure drops. Below the ball, the spin causes air motion opposite the direction of motion of the ball. The effective speed of the lower part of the ball and of the air around it reduces hence pressure increases. This higher pressure pushes the ball up.
(5) State Pascal’s principle of transmission of pressure in liquids.
Pascal’s principle (Pascal’s law) states that for a liquid at rest and enclosed in a container, pressure applied at one point is equally transmitted throughout the liquid.
Example 5 KCSE 2017
(1) State the reason why the speed of water at the narrow section of a river is higher than at the wider section. (1 mark)
Continuity equation:

The speed of water in the thinner pipe must therefore be higher than in the wider pipe so as to maintain a constant volume flow rate of water.
(2)The figure shows a hydraulic brake system
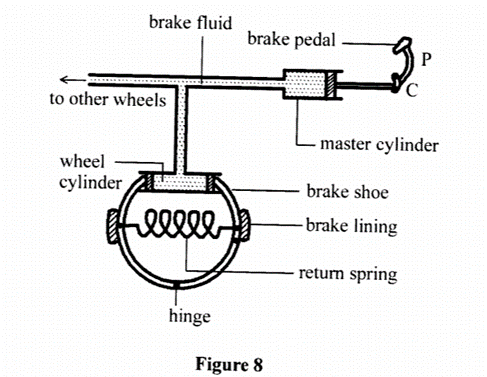
Describe how the systems works (5 marks)
Force applied to liquid in master cylinder generates pressure (Pressure = force/area) in the master cylinder. This pressure is transmitted uniformly through the fluid to the wheel cylinder. The force generated (force = pressure x area) acts on the brake shoe which in turn presses the brake pads which then stop the wheel from rotating.
Revision Questions
KCSE 2016
(1) An aeroplane is moving horizontally through still air at a uniform speed. It is observed that when the speed of the plane is increased, its height above the ground increases. State the reasons for this observation. (1 mark)
(2) Figure 6 shows parts A, B and C of a glass tube.
State with a reason the part of the tube in which the pressure will be lowest when air is blown through the tube from A towards C. (2 marks)
(3) Figure 8 shows two cylinders of different cross-sectional areas connected with a tube. The cylinders contain an incompressible fluid and are fitted with pistons of cross-sectional areas 4 cm2 and 24 cm2.
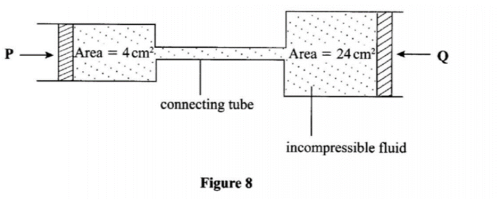
Opposing forces P and Q are applied to the pistons such that the pistons do not move. If the pressure on the smaller piston is 5N/cm2, determine force Q. (2 marks)
KCSE 2015
(1) State two factors that determine the pressure at a point in a liquid. (2 marks)
(2) A student wearing sharp pointed heeled shoes is likely to damage a soft wooden floor. Explain. (2 marks)
(3) Figure 5 shows air flowing through a pipe of different cross—section areas. Two pipesA and B are dipped into water.
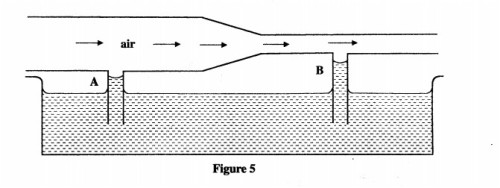
Explain the cause of the difference in the levels of water in the pipes A and B. (2 marks)
(4) Figure 9 shows a hydraulic lift system. The radius of the small piston is 3 cm while that of the larger piston is 9 cm. A force of 90 N is applied to the smaller piston.
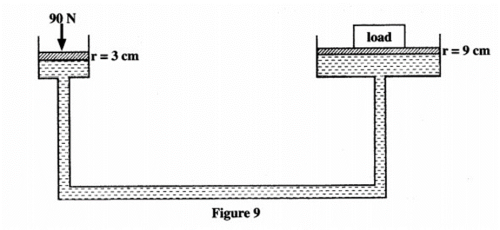
Determine the:
(i) maximum load that can be lifted. (3 marks)
(ii) efficiency of the system. (3 marks)
KCSE 2014
(1) Figure 3 shows two cylinders of different cross-sectional areas connected with a tube. The cylinders contain an incompressible fluid and are fitted with pistons of cross-sectional areas 4 cm2 and 24 cm2.
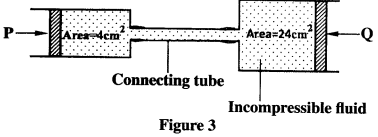
Opposing forces P and Q are applied to the pistons such that the pistons do not move. if the pressure on the smaller piston is 5 N cm’. Determine force Q. (2 marks)
(2) Figure 7 shows an incompressible fluid flowing through a pipe, AI and AZ are the cross-sectional areas of the pipes in the larger section and smaller section of the pipe respectively, while V1 and V2 are speeds of the fluid at the two sections of the pipe.
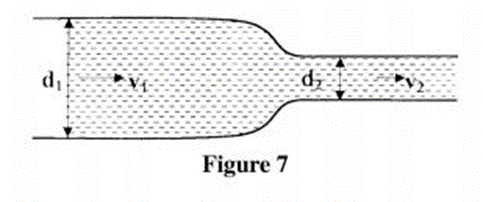
Derive an expression for the ratio of the speeds % in terms of AI and A2. (2 marks)
KCSE 2013
(1) Figure 2 shows some air trapped by mercury in a glass tube. The tube is inverted in a dish containing mercury.
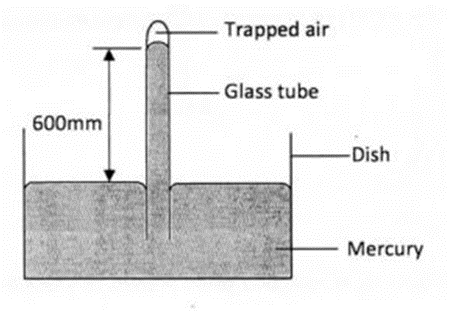
Given that the atmospheric pressure is 760 mmHg and the height of mercury column in the tube is 600 mm, determine the pressure of the air trapped in the tube in mmHg. (3 marks)
(2) Explain why brakes fail in a hydraulic braking system when air gets into the system.
KCSE 2012
(1) An aeroplane is moving horizontally through still air at a uniform speed. It is observed that when the speed of the plane is increased, its height above the ground increases. State the reason for this observation. (1 mark)
(2) Figure 5 shows parts A, B and C of a glass tube. 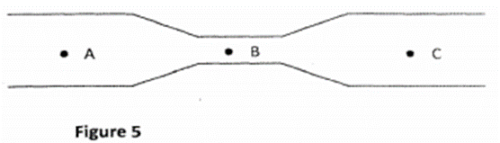
State with a reason the part of the tube in which the pressure will be lowest when air is blown through the tube from A towards C. (2 marks)
(3) In an experiment to demonstrate atmospheric pressure, a plastic bottle is partially filled with hot water and the bottle is then tightly corked. After sometime the bottle starts to get deformed.
a)State the purpose of the hot water. (1 mark)
b)State the reason why the bottle gets deformed. (1 mark)
c)Explain your answer in c (b) (2 marks)
(4) a)A lift pump can lift water to a maximum height of 10 m. Determine the maximum height to which the pump can raise paraffin.
(take density of paraffin 800 kgm-3 and density of water as 1000 kgm-3).
b) State one factor that determines the height to which a force pump can lift water. (1 mark)
KCSE 2011
(1) Figure 7 shows part of a petrol engine, in which air flowing under atmospheric pressure passes into a constriction, where it mixes with petrol. The mixture then flows into a combustion cylinder.
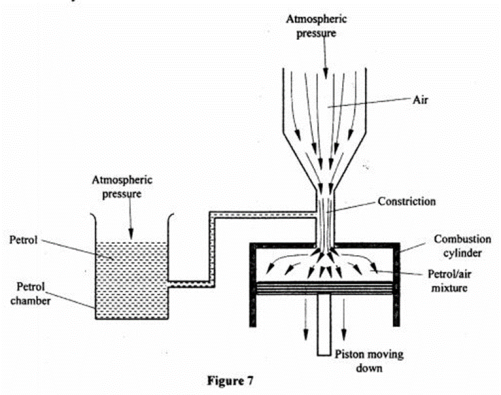
Explain what causes the petrol to move from the petrol chamber to the air stream in the constriction when the piston is moved downwards. (2 marks)
(2) Figure 9 shows a syringe full of water. It has two identical holes A and B drilled along it s cylinder. The cylinder nozzle is closed.
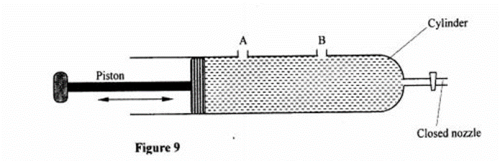
State with a reason how the speeds of the jets of water from A and B compare when the piston is pushed into the cylinder. (2 marks)
KCSE 2010
(1) Figure 4 shows a horizontal tube with two vertical tubes x and y. water flows through the horizontal tube from right to left. The water level in tube x is higher than water level in tube y.
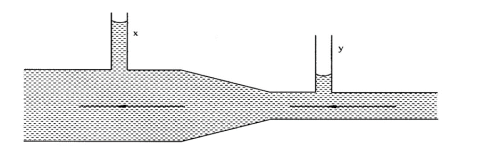
Explain this observation (2 marks)


1 Comment(s)
Esther Kasim (Tue, 19th Mar 2024, 10:28 AM)
I like the revised version mummy quite impressive
Reply